Cours sur le produit scalaire dans le plan

« Chapitre 7 : CALCUL VECTORIEL ET PRODUIT SCALAIRE I) DEFINITIONS DU PRODUIT SCALAIRE A.

Définition avec le cosinus 𝐶 Définition : Soient 𝑢 ⃗⃗⃗ et 𝑣 ⃗⃗⃗ deux vecteurs. ̂ où 𝑢 ⃗⃗⃗⃗⃗ . On appelle angle géométrique noté (𝑢 ⃗ , 𝑣 ), l’angle 𝐵𝐴𝐶 ⃗ = ⃗⃗⃗⃗⃗ 𝐴𝐵 et 𝑣 = 𝐴𝐶 ̂ 𝐵𝐴𝐶 𝐴 𝐵 Définition : Soient 𝑢 ⃗⃗⃗ et 𝑣 ⃗⃗⃗ deux vecteurs. ⃗ •𝒗 ⃗ , le réel défini par On appelle produit scalaire de 𝑢 ⃗⃗⃗ et 𝑣 ⃗⃗⃗ , noté 𝒖 ⃗ •𝒗 ⃗ = ||𝑢 ➢ 𝒖 ⃗ || × ||𝑣 || × cos (𝑢 ⃗ , 𝑣 ) lorsque les deux vecteurs 𝑢 ⃗⃗⃗ et 𝑣 ⃗⃗⃗ sont non nuls, avec ||𝑢 ⃗ || , ||𝑣 || les normes des vecteurs 𝑢 ⃗⃗⃗ et 𝑣 ⃗⃗⃗ . ⃗ •𝒗 ⃗ = 0 lorsque qu’au moins un des deux vecteurs 𝑢 ➢ 𝒖 ⃗⃗⃗ et 𝑣 ⃗⃗⃗ est nul. ⃗⃗⃗⃗⃗ alors le produit scalaire de 𝑢 Remarque : si 𝑢 ⃗⃗⃗ = ⃗⃗⃗⃗⃗ 𝐴𝐵 et 𝑣 ⃗⃗⃗ = 𝐴𝐶 ⃗⃗⃗ et 𝑣 ⃗⃗⃗ s’écrit aussi : ̂ . 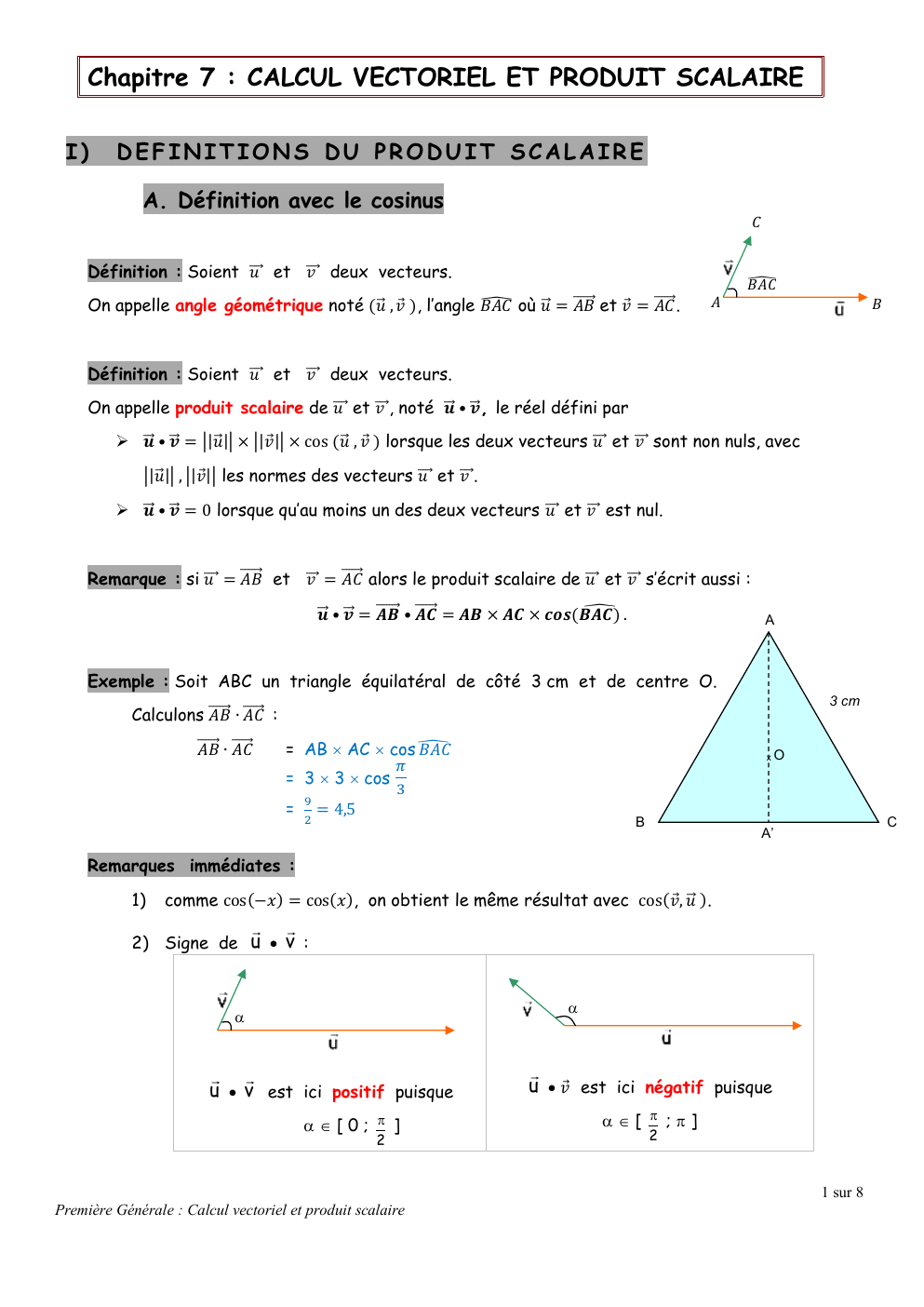⃗⃗⃗⃗⃗⃗ • 𝑨𝑪 ⃗⃗⃗⃗⃗ = 𝑨𝑩 × 𝑨𝑪 × 𝒄𝒐𝒔(𝑩𝑨𝑪) ⃗ •𝒗 ⃗ = 𝑨𝑩 𝒖 A Exemple : Soit ABC un triangle équilatéral de côté 3 cm et de centre O. 3 cm ⃗⃗⃗⃗⃗ : Calculons ⃗⃗⃗⃗⃗ 𝐴𝐵 ∙ 𝐴𝐶 ⃗⃗⃗⃗⃗ ∙ 𝐴𝐶 ⃗⃗⃗⃗⃗ 𝐴𝐵 = AB  AC  cos ̂ 𝐵𝐴𝐶 = 3  3  cos = 9 2 xO 𝜋 3 = 4,5 B C A’ Remarques immédiates : 1) comme cos(−𝑥) = cos(𝑥), on obtient le même résultat avec cos(𝑣 , 𝑢 ⃗ ).   2) Signe de u • v :     u • v est ici positif puisque [0;  ] 2  u • 𝑣 est ici négatif puisque [  ;] 2 1 sur 8 Première Générale : Calcul vectoriel et produit scalaire Cas particuliers : ‖𝒖 ⃗ ‖ × ‖𝒗 ⃗ ‖ si les vecteurs ont le même sens. ⃗ •𝒗 ⃗ = Si 𝑢 ⃗ et 𝑣 sont colinéaires 𝒖 ⃗ ‖ × ‖𝒗 ⃗ ‖ si les vecteurs ont un sens contraire. −‖𝒖 ⃗ •𝒖 ⃗ = 𝒖 ⃗ ² = ‖𝒖 ⃗ ‖ ². On appelle « carré scalaire » le réel : 𝒖 B.

Définition avec les normes 1 2 ⃗ •𝒗 ⃗ = ( ‖𝑢 Théorème : Soient 𝑢 ⃗⃗⃗ et 𝑣 ⃗⃗⃗ deux vecteurs.

On a 𝒖 ⃗ + 𝑣⃑ ‖ ² − ‖𝑢 ⃗ ‖ ² − ‖𝑣 ‖ ² ). → → Exemple : Soit ABC un triangle équilatéral de côté a.

Calculons 𝑩𝑨 • 𝑨𝑪 . → → 𝑩𝑨 • 𝑨𝑪 = → 1 (‖𝐵𝐴 2 = → 1 (‖𝐵𝐶 ‖ ² 2 = 1 2 ( BC² - BA² - AC² ) = 1 2 ( a² - a² - a² ) = − → → → + 𝐴𝐶 ‖ ² − ‖𝐵𝐴‖ ² − ‖𝐴𝐶 ‖ ²) A → → − ‖𝐵𝐴‖ ² − ‖𝐴𝐶 ‖ ²) a a B a 𝑎² C 2 C.

Définition.... »