Chapitre de Terminale spécialité – Continuité et convexité d’une fonction – Programme 2020

« Chapitre de Terminale spécialité – Continuité et convexité d’une fonction – Programme 2020 I. Continuité 1.

Continuité d’une fonction Définition Soit 𝑓 une fonction définie sur un intervalle 𝐼. Soit 𝑎∈𝐼 .

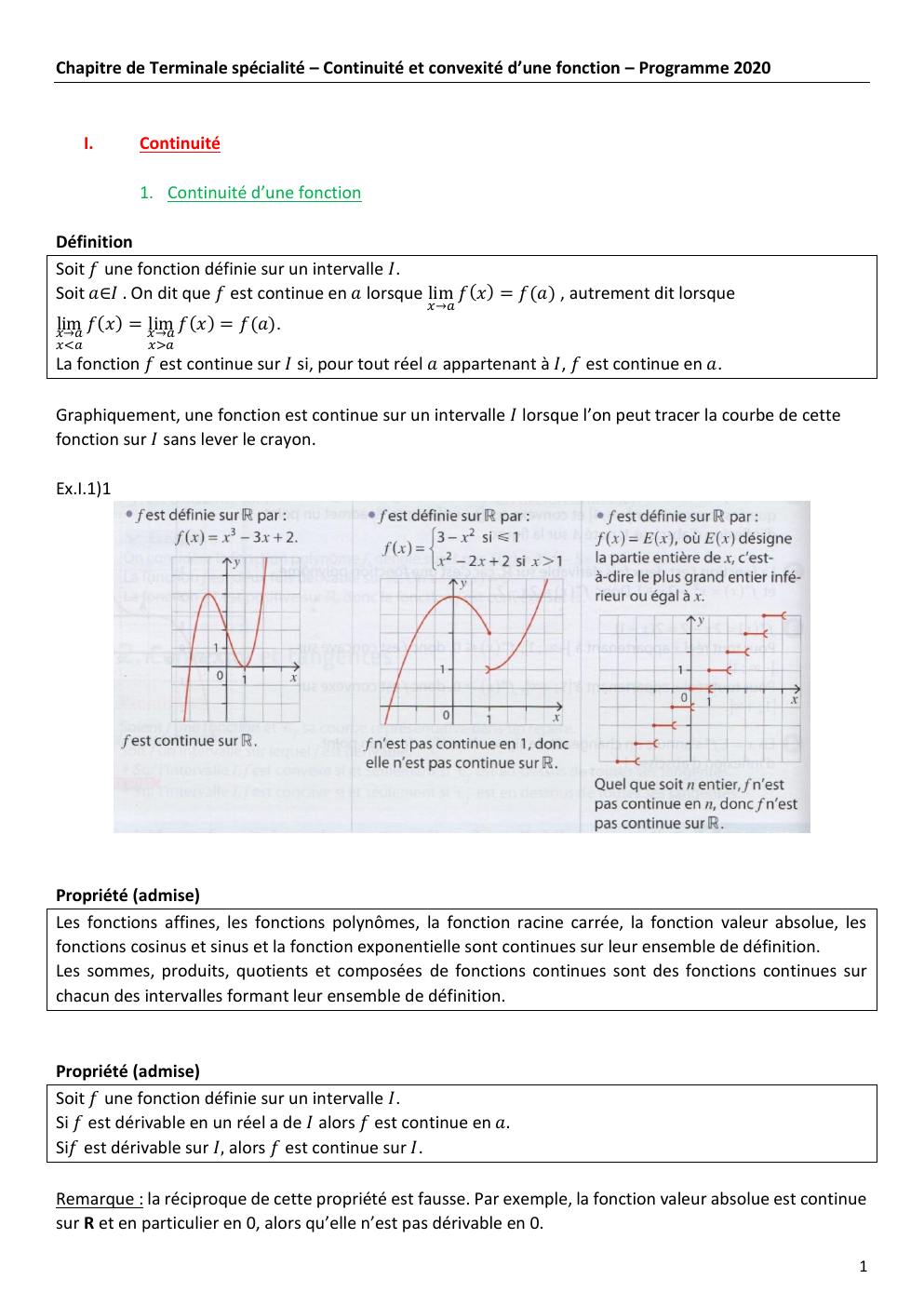
On dit que 𝑓 est continue en 𝑎 lorsque lim 𝑓 (𝑥 ) = 𝑓(𝑎) , autrement dit lorsque 𝑥→𝑎 lim 𝑓 (𝑥 ) = 𝑥→𝑎 lim 𝑓 (𝑥 ) = 𝑓(𝑎). 𝑥→𝑎 𝑥𝑎 La fonction 𝑓 est continue sur 𝐼 si, pour tout réel 𝑎 appartenant à 𝐼, 𝑓 est continue en 𝑎. Graphiquement, une fonction est continue sur un intervalle 𝐼 lorsque l’on peut tracer la courbe de cette fonction sur 𝐼 sans lever le crayon. Ex.I.1)1 Propriété (admise) Les fonctions affines, les fonctions polynômes, la fonction racine carrée, la fonction valeur absolue, les fonctions cosinus et sinus et la fonction exponentielle sont continues sur leur ensemble de définition. Les sommes, produits, quotients et composées de fonctions continues sont des fonctions continues sur chacun des intervalles formant leur ensemble de définition. Propriété (admise) Soit 𝑓 une fonction définie sur un intervalle 𝐼. Si 𝑓 est dérivable en un réel a de 𝐼 alors 𝑓 est continue en 𝑎. Si𝑓 est dérivable sur 𝐼, alors 𝑓 est continue sur 𝐼. Remarque : la réciproque de cette propriété est fausse.

Par exemple, la fonction valeur absolue est continue sur R et en particulier en 0, alors qu’elle n’est pas dérivable en 0. 1 2.

Continuité et suites Théorème du point fixe (admis) Soit 𝑓 une fonction définie sur un intervalle 𝐼, L un réel de 𝐼.

Soit (Un) une suite à valeur dans 𝐼 définie par un premier terme et telle que Un+1 = 𝑓(Un) pour tout entier naturel n. Si (Un) converge vers L et si 𝑓 est continue en L, alors la limite L de la suite est solution de l’équation 𝑓(L) = L Ex.I.2)1 1 Soit (Un) la suite définie par son premier terme U 0= 1 et par la relation de récurrence U n+1 = 2 Un +2 pour tout entier naturel n.

Construire les 4 premiers termes de la suite sur le graphique ci-dessous. Conjecturer le sens de variation et la limite de cette suite. On admet que (Un) est croissante et majorée par 4 (peut se démontrer par récurrence) En déduire qu’elle converge et préciser sa limite L. 2 II. Théorème des valeurs intermédiaires 1.

Cas d’un intervalle fermé Théorème des valeurs intermédiaires (admis) Soit 𝑓 une fonction continue sur un intervalle [𝑎 ; 𝑏]. Pour tout réel k compris entre 𝑓(𝑎) et 𝑓(𝑏), l’équation 𝑓(𝑥) = k admet au moins une solution dans l’intervalle [𝑎; 𝑏]. Remarque : cela signifie que lorsque 𝑥 varie de 𝑎 à 𝑏, 𝑓(𝑥) prend toutes les valeurs intermédiaires comprises entre 𝑓(𝑎) et 𝑓(𝑏). En particulier : Soit 𝑓 une fonction continue sur [𝑎; 𝑏].

Si 𝑓(𝑎) et 𝑓(𝑏) sont de signe contraire, alors il existe au moins une solution sur [𝑎; 𝑏] à l’équation 𝑓(𝑥 ) = 0 Théorème de LA valeur intermédiaire (admis) Soit 𝑓 une fonction continue et strictement monotone sur un intervalle [𝑎; 𝑏]. Pour tout réel k compris entre 𝑓(𝑎) et 𝑓(𝑏), l’équation 𝑓(𝑥) = k admet une unique solution dans l’intervalle [𝑎; 𝑏]. Convention : Dans un tableau de variations, les flèches obliques indiquent que la fonction est continue et strictement monotone sur l’intervalle considéré. 3 Ex.II.1)1 Soit 𝑓 la fonction définie sur R par 𝑓 (𝑥 ) = 𝑒 𝑥 + 𝑥 − 2. a.

Démontrer que l’équation 𝑓 (𝑥 ) = 1 admet une unique solution α sur [0 ; 1]. b.

Déterminer à l’aide de la calculatrice un encadrement de α à 10-2 près. Méthode graphique : Affiche à l’écran de la calculatrice les courbes d’équations 𝑦 = 𝑒 𝑥 + 𝑥 − 2 et 𝑦 = 1 puis afficher les coordonnées du point d’intersection de ces deux courbes.

En déduire un encadrement de α à 10-2 près. Méthode par balayage : Afficher le tableau de valeurs de la fonction 𝑓 sur [0 ;1] avec un pas de 0,1.

En déduire un encadrement de α à 10-1 près.

Afficher le tableau de valeurs de la fonction 𝑓 sur ce nouvel intervalle avec un pas de 0,01.

En déduire un encadrement de α à 10-2 près. 2.

Extension à d’autres intervalles Les deux.... »