La nécessité d'accepter des postulats invérifiables
La nécessité d'accepter des postulats invérifiables
Mais, alors comment pouvons-nous être assurés que cette idée est bien vraie ? Devons-nous admettre que toute notre science ne repose que sur des hypothèses ? La réponse de Pascal: «En poursuivant les recherches de plus en plus, on arrive nécessairement à des mots primitifs qu'on ne peut plus définir, et à des principes si claires qu'on n'en trouve plus qui le soient davantage pour servir à leur preuve. D'où il paraît que les hommes sont dans une impuissance naturelle et immuable à traiter quelque science que ce soit dans un ordre parfaitement accompli.» («De l'esprit de géométrie»).
Même, en mathématique, on est obligé de recourir à des propositions premières ou initiales qu'on admet comme vraies, sans qu'on puisse les démontrer = «Par un point extérieur à une droite, on ne peut faire passer qu'une seule droite parallèle à cette droite», "Par deux points ne peut passer qu'une droite", "La ligne droite est le plus court chemin d'un point à un autre". (Euclide) = axiomes. On les tient pour évidente sans pouvoir la démontrer.
Dans "Les éléments", on trouve en particulier les cinq axiomes qui fondent les bases de la géométrie.
Axiome 1 :
Par deux points distincts, il passe une droite et une seule.

Axiome 2 :
Tout segment est prolongeable en une droite.

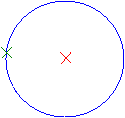
Axiome 3 :
Deux points distincts étant donnés,
il passe un cercle et un seul de centre le premier point et passant par le second.
Axiome 4 :
Tous les angles droits sont égaux entre eux.
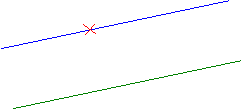
Axiome 5 :
Par un point extérieur à une droite, il passe une droite et une seule parallèle à la droite donnée.
Liens utiles
- La liberté consiste-t-elle à accepter la nécessité ?
- Aide à la dissertation: libre arbitre et nécessité
- Quelle réflexion cette moralité de LA FONTAINE vous inspire-t-elle concernant la nécessité de l’imagination dans l’exercice de la pensée ?
- En quoi les espaces maritimes sont-ils tiraillés entre recherche d’appropriation, nécessité de protection et maintien de la liberté de circulation ?
- « Poésie ! ô trésor ! perle de la pensée! [...] 0 toi ! des vrais penseurs impérissable amour ! Comment se garderaient les profondes pensées, Sans rassembler leurs feux dans ton diamant pur Qui conserve si bien leurs splendeurs condensées ? Ce fin miroir solide, étincelant et dur, Reste des nations mortes, durable pierre Qu'on trouve sous ses pieds lorsque dans la poussière On cherche les cités sans en voir un seul mur. » (Vigny, La Maison du Berger.) Vous dégagerez la définition de la
