Grand oral Math Logarithme

« Grand Oral : MATHS : - Peut-on se fier au résultat d’un test diagnostique ? Introduction : Des avancées majeures ont été réalisées en médecine ces dernières décennies.

En effet, les tests de diagnostiques de dépistage rapide ont permis de détecter avec une grande fiabilité des maladies infectieuses comme l’angine, le paludisme, ou encore le VIH.

Le patient peut être positif (identifiant le sujet comme étant malade) ou négatif (sujet non malade). Peut-on se fier au résultat d’un test diagnostique ? Peut-on observées des erreurs telles les faux-négatifs et les faux-positifs ? Après avoir établi le diagnostic d’un patient, nous nous intéresserons à la sensibilité et à la spécificité d’un test diagnostique et à l’importance des valeurs prédictives positives et négatives. I - Diagnostic d’un patient : Tout d’abord, on sait qu’un test ne peut pas être interprété de manière univoque : certains patients peuvent avoir un test positif alors qu’ils ne sont pas malades (faux positifs), et d’autres, au contraire, peuvent avoir un test négatif alors qu’ils sont malades (faux négatifs). Prenons une situation simple : une personne vient de passer un test de dépistage d’une maladie rare.

On sait qu’elle ne touche que 0,1 % de la population.

Le médecin lui annonce que le résultat du test est positif.

Le patient demande au médecin si le test est fiable.

Sa réponse est sans appel : « Si vous êtes malade, le test est positif dans 90% des cas et si vous n’êtes pas malades, il est négatif dans 97 % des cas ».

On pose la question suivante : « quelle est la probabilité que cette personne soit effectivement malade ? ».

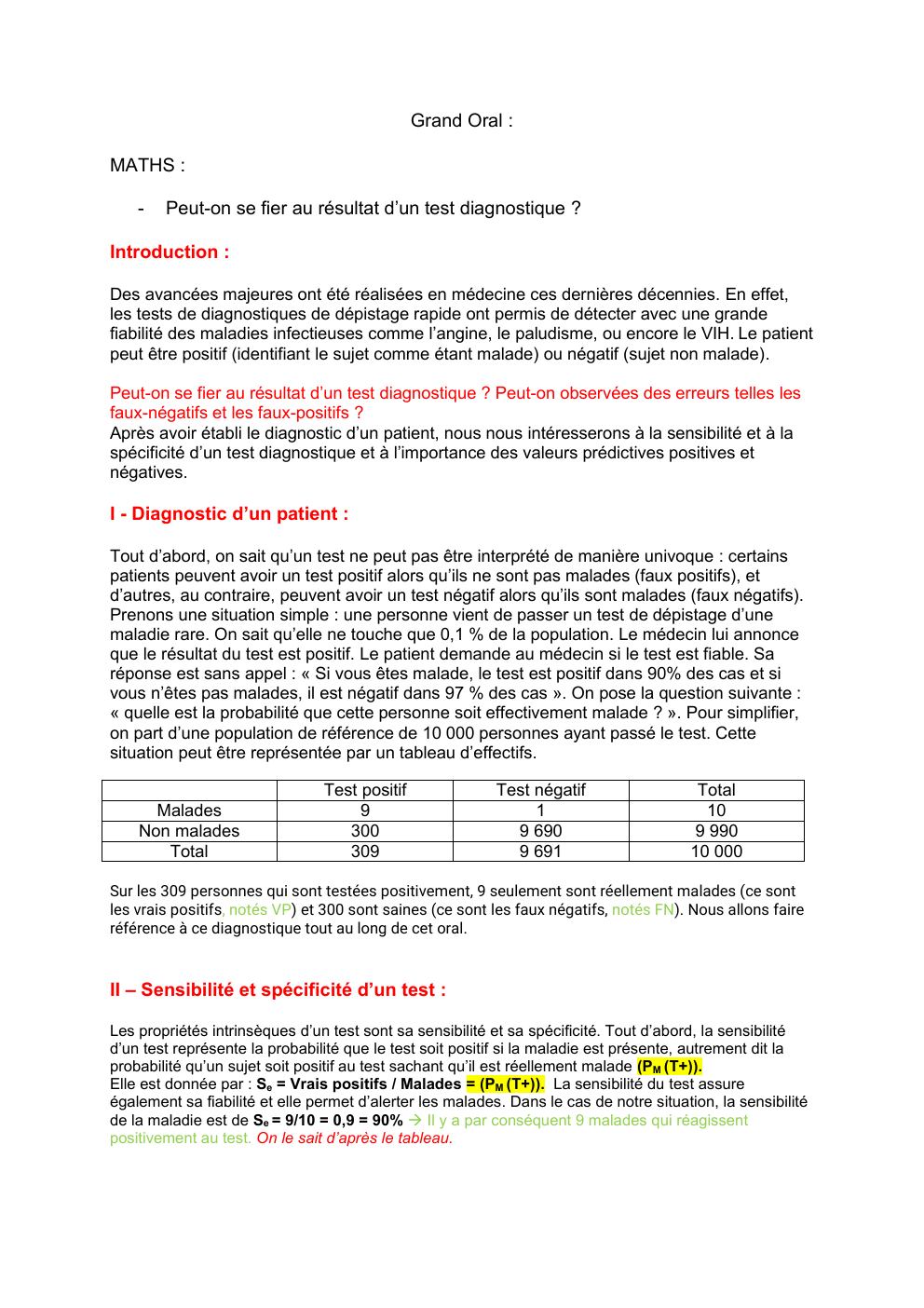
Pour simplifier, on part d’une population de référence de 10 000 personnes ayant passé le test.

Cette situation peut être représentée par un tableau d’effectifs. Malades Non malades Total Test positif 9 300 309 Test négatif 1 9 690 9 691 Total 10 9 990 10 000 Sur les 309 personnes qui sont testées positivement, 9 seulement sont réellement malades (ce sont les vrais positifs, notés VP) et 300 sont saines (ce sont les faux négatifs, notés FN).

Nous allons faire référence à ce diagnostique tout au long de cet oral. II – Sensibilité et spécificité d’un test : Les propriétés intrinsèques d’un test sont sa sensibilité et sa spécificité.

Tout d’abord, la sensibilité d’un test représente la probabilité que le test soit positif si la maladie est présente, autrement dit la probabilité qu’un sujet soit positif au test sachant qu’il est réellement malade (PM (T+)). Elle est donnée par : Se = Vrais positifs / Malades = (PM (T+)).

La sensibilité du test assure également sa fiabilité et elle permet d’alerter les malades.

Dans le cas de notre situation, la sensibilité de la maladie est de Se = 9/10 = 0,9 = 90% → Il y a par conséquent 9 malades qui réagissent positivement au test.

On le sait d’après le tableau. Puis, la spécificité d’un test représente la probabilité que le test soit négatif si la maladie n’est pas présente, autrement dit la probabilité qu’un sujet soit négatif au test sachant qu’il est réellement non malade (PM « barre » (T-)). Elle est donnée par : Sp = Vrais négatifs /Non Malades = (PM « barre » (T-)).

De plus, elle représente la capacité d’un test à ne pas alerter faussement les non-malades.

Si nous reprenons notre situation, la spécificité du test de la maladie rare est de Sp = 9 690/9 990 = 0,969 = 97 % → Il y a 9 690 test négatif chez une personnes saines, et donc 300 tests positifs chez ces 9 990 personnes saines. Ces deux caractéristiques sont calculées.... »