Histoire du calcul différentiel (TPE)

« U~LANCACE REVOLUTIONNAIRE Fondé sur l'utilisation de grandeurs infinitésimales, le calcul différentiel peut paraître éloigné de la réalité de tout un chacun .

Cependan~ il a été crucial dans la résolution de nombreux problèmes mathématiques , auparavant insolubles , liés à des approches pratiques telles que le calcul de vitesses et d 'accélérations.

Utile dans un ensemble de domaines (optique, mathématiques , astronomie ...

), le calcul différentiel intervient chaque fois qu'un certain nombre de grandeurs physiques varient les unes par rapport aux autres, c'est-à-dire En leur apportant une solution générale , tout le temps.

Sans lui, il est certain que la révolution scientifique et industrielle n'aurait pas eu lieu.

Leibniz va montrer que chacun de ces deux problèmes était le -----------~ réciproque de l'autre .

UNE HISTOIRE CONTROVERSÉE Dans l'Antiquité, deux types généraux de problèmes géométriques se sont posés , pour lesquels il ne semblait exister que des solutions particulières : le calcul des tangentes et le calcul des quadratures (à la base, calcul de surfaces et volumes) .

Bien longtemps après , l'astronome lohflnnes Kepler se trouve confronté à un problème similaire qui paraît insoluble .

En effe~ après avoir découvert que la trajectoire des planètes est elliptique, il tente de calculer la surface d 'un secteur elliptique mais n'arrive qu'à une approximation.

il lance , dans son ouvrage " Astronomie nouvelle », un appel aux géomètres pour trouver un nouvel outil mathématique afin de résoudre ce problème .

Des savants comme Pierre de Fermat, Blaise Pascal , Isaac Newton , Gottfried leibniz et bien d'autres se lancent dans cette recherche .

C'est finalement Leibniz qui découvre le calcul différentiel et intégral.

Cependan~ il existe une polémique à ce suje~ certains pensant que Newton aurait inventé un calcul équivalent à celui de Leibniz, appelé calcul des fluxions.

Certes, Leibniz a le premier publié ses résultats en 1684, mais Newton l'avait accusé de plagiat.

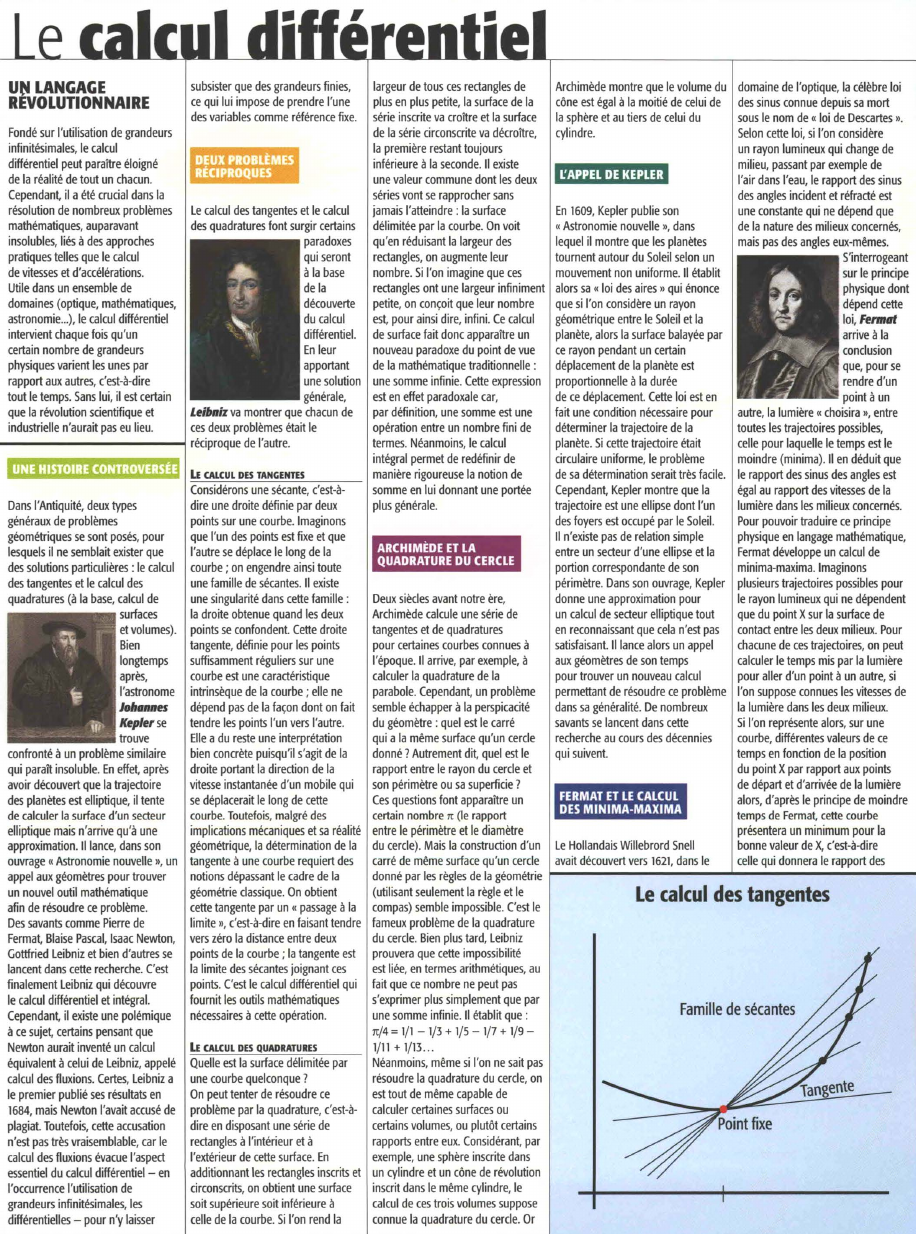
Toutefois, cette accusation n 'est pas très vraisemblable , car le calcul des fluxions évacue l'aspect essentiel du calcul différentiel -en l'occurrence l'utilisation de grandeurs infinités imales, les différentielles- pour n 'y laisser LE CALCUL DES TANGENTES Considérons une sécante , c'est -à­ dire une droite définie par deux points sur une courbe.

Imaginons que l'un des points est fixe et que l'autre se déplace le long de la courbe ; on engendre ainsi toute une famille de sécantes .

Il existe une singularité dans cette famille : la droite obtenue quand les deux points se confondent.

Cette droite tangente, définie pour les points suffisamment réguliers sur une courbe est une caractéristique intrinsèque de la courbe ; elle ne dépend pas de la façon dont on fait tendre les points l'un vers l 'autre .

Elle a du reste une interprétation bien concrète puisqu'il s 'agit de la droite portant la direction de la vitesse instantanée d 'un mobile qui se déplacerait le long de cette courb e.

Toutefoi s, malgr é des implications mécaniques et sa réalité géométrique , la détermination de la tangente à une courbe requiert des notions dépassant le cadre de la géométrie classique .

On obtient cette tangente par un " passage à la limite », c 'est-à-dire en faisant tendre vers zéro la distance entre deux points de la courbe ; la tangente e st la limite des sécantes joignant ces points .

C'est le calcul différentiel qui fournit les outils mathématiques nécessaires à cette opération .

LE CALCUL DES QUADRATURES Quelle est la surface délimitée par une courbe quelconque? On peut tenter de résoudre ce problème par la quadrature , c'est-à­ dire en disposant une série de rectangles à !Intérieur et à l ' extérieur de cette surface .

En additionnant les rectangles inscrits et circonscrits, on obtient une surface soit supérieure soit inférieure à celle de la courbe .

Si l'on rend la largeur de tous ces rectangles de plus en plus petite , la surface de la série inscrite va croître et la surface d e la série circonscrite va d écroître , la première restant toujours inférieure à la seconde .

Il existe une valeur commune dont le s deux série s vont se rapproche r sans jamais l'atteindre : la surface d élimitée par la courbe .

On voit qu'en réduisant la largeur des rectangles, on augmente leur nombre .

Si l'on imagine que ces rectangles ont une largeur infiniment petite, on conçoit que leur nombre ~ pour ainsi dire, infini .

Ce calcul de surface fait donc appara ître un nouveau parado x e du point de vue de la mathématique traditionnelle : une somme infinie .

Cette expression est en effet paradoxale car, par définit ion, une somme est une opération entre un nombre fini de term es.

Néanmoins, le calcul intégral permet de redéfinir de manière rigoureuse la notion de somme en lui donnant une portée plus générale .

ARCHIMÈDE ET LA QUADRATURE DU CERCLE Archim ède montre que le volume du cône est égal à la moitié de celui de la sphère et au tiers de celui du cylindre .

"MJIH:W!U domaine de l 'optique , la célèbre loi des sinu s connue depuis sa mort sous le nom de " loi de Descartes ».

Selon cette loi, si l'on considère un rayon lumineux qui change de milieu, passant par exemple de l'air dans l'eau , le rapport des sinus des angles incident et réfracté est En 1609 , Kepler publie son une constante qui ne dépend que " Astronomie nouvelle », dans de la nature des milieu x concernés , lequel il montre que les planètes mais pas des angles eux-mêmes .

tournent autour du Sole il selon un S'interrogeant mouvement non uniforme .

Il établit sur le principe alors sa " loi des aires » qui énonce physique dont que si l 'on considère un rayon dépend cette géom étrique entr e le Soleil et la loi, Fermtlt plan ète, alors la surface balayée par arrive à la ce rayon pendant un certain conclusion déplacement de la planète est que, pour se proportionnelle à la durée rendre d'un de ce déplacement.

Cette loi est en point à un fait une condition nécessaire pour autre , la lumière " choisira », entre déterminer la trajectoire de la toutes les trajectoires possibles, planète .

Si cette trajectoire était celle pour laquelle le temps est le circulaire uniforme , le problème moindre (minima) .

Il en déduit que de sa d étermination serait très facile .

le rapport des sinus des angles est Cependant , Kepler montre que la égal au rapport des vitesses de la trajectoire est une ellipse dont l'un lumière dans les milieux concernés.

des foyers est occupé par le Soleil.

Pour pouvoir traduire ce principe Il n 'existe pas de relation simple physique en langage mathématique, entre un secteur d 'une ellipse et la Fermat développe un calcul de portion correspondante de son minima -maxima .

Imaginons périmètre.

Dans son ouvrage , Kepler plusieurs trajectoires possibles pour Deux siècles avant notre ère, donne une approximation pour le rayon lumineux qui ne dépendent Archimède calcule une série de un calcul de secteur elliptique tout que du point X sur la surface de tangentes et de quadratures en reconnais sant que cela n 'est pas contact entre les deux milieux .

Pour pour certaines courbes connues à satisfaisant il lance alors un appel chacune de ces trajectoires, on peut l'époque .

il arrive , par exemple , à aux géomètres de son temp s calculer le temps mis par la lumière calculer la quadrature de la pour trouver un nouveau calcul pour aller d 'un point à un autre , si parabole .

Cependant, un problème permettant de résoudre ce problème l'on suppose connues les vitesses de semble échapper à la perspicacité dans sa généralité .

De nombreu x la lumière dans les deux m ilieux.

du géomètre :quel est le carré savants se lancent dans cette Si l'on représente alors , sur une qui a la même surface qu'un cercle recherche au cours des décennies courbe , différentes valeurs de ce donné ? Autrement di~ quel est le qui suivent.

temps en fonction de la position rapport entre le rayon du cercle et du point X par rapport aux points son périmètre ou sa superficie? de départ et d'arrivée de la lumière Ces questions font appara ître un alors , d 'après le principe de moindre certain nombre " (le rapport temps de Fermat , cette courbe entre le périmètre et le diamètre présentera un minimum pour la du cercle ).

Mais la construction d 'un Le Hollandais Willebrord Snell bonne valeur de X, c'est-à-dire carré de même surface qu'un cercle avait d écouvert vers 1621 , dans le celle qui donnera le rapport des donné par les règles de la géométri e f-----------...1.-----------­ (utilisant seulement la règle et le compas ) semble imposs ible.

C'est le fameux problème de la quadrature du cercle .

Bien plus tard , leibniz prouvera que cette impo ssibilité est liée, en termes arithmétiques, au fait que ce nombre ne peut pas s'exprimer plus simplement que par une somme infinie .

Il établit que : 7t/ 4 = l/1 -1/ 3 + l/5 -l/7 + l/9 - 1/11 + l/13 ...

Néanmoin s , même si l'on ne sait pas résoudre la quadrature du cercle, on est tout de même capable de calculer certaines surface s ou certains volumes, ou plutôt certains rapports entre eux.

Con sidérant , par e xemple , une sphère inscrite dans un cylindre et un cône de révolution inscrit dans le même cylindre, le calcul de ces trois volume s suppo se connue la quadrature du cercle.

Or Le calcul des tangentes Famille de sécantes. »